
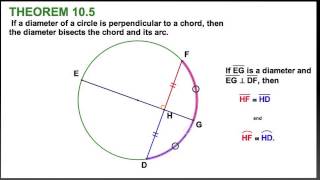
Read more about this in our circumference calculator and arc length calculator. The same method may be used to find arc length – all you need to remember is the formula for a circle's circumference. So, what's the area for the sector of a circle:įrom the proportion, we can easily find the final sector area formula: Intersecting Chords Theorem: If two chords intersect inside a circle so that one is divided into segments of length a and b and the other into segments of length c c and d d then ab cd a b c d. Then, we want to calculate the area of a part of a circle, expressed by the central angle.įor angles of 2π (full circle), the area is equal to πr²:
#DEFINITION OF CHORD GEOMETRY FULL#
The full angle is 2π in radians, or 360° in degrees, the latter of which is the more common angle unit. The area of a circle is calculated as A = πr². All you need to remember is the circle area formula (and we bet you do!): This is why gliders have long slender wings.The formula for sector area is simple – multiply the central angle by the radius squared, and divide by 2:īut where does it come from? You can find it by using proportions.

Induced drag is most significant at low airspeeds. The ratio of the length (or span) of a rectangular-planform wing to its chord is known as the aspect ratio, an important indicator of the lift induced drag the wing will create. (For wings with planforms that are not rectangular, the aspect ratio is calculated as the square of the span divided by the wing planform area.) Wings with higher aspect ratios will have less induced drag than wings with lower aspect ratios. Any shape other than a simple trapezoid requires evaluation of the above integral.
#DEFINITION OF CHORD GEOMETRY MAC#
Note that the figure above implies that the MAC occurs at a point where leading or trailing edge sweep changes. In particular, the position of the centre of gravity (CG) of an aircraft is usually measured relative to the MAC, as the percentage of the distance from the leading edge of MAC to CG with respect to MAC itself. Therefore, not only the length but also the position of MAC is often important. The pressure distribution over the entire wing can be reduced to a single lift force on and a moment around the aerodynamic center of the MAC.
The MAC is a two-dimensional representation of the whole wing. Where y is the coordinate along the wing span, S is the wing area, b is the span of the wing, and cis the chord at the coordinate y. The 57 mean it is chord 1 times the mean chord length. The distance between the leading and trailing edge of the wing, measured parallel to the normal airflow over the wing, is known as the chord. The value has also an interesting geometric meaning length of the two-dimensional shape. Mean aerodynamic chord (MAC) is defined as: Mean Aerodynamic Chord is the average chord length of a tapered, swept wing. In large aircraft, centre of gravity limitations and the actual centre of gravity are often expressed in terms of percent MAC. The average length of the chord is known as the Standard mean chord (SMC). As a consequence, the chord also changes along the span of the wing.
The width of the wing is greatest where it meets the fuselage at the wing root and progressively decreases toward the tip. Most commercial transport airplanes have wings that are both tapered and swept with the result that the width of the wing changes along its entire length. If the leading edge and trailing edge are parallel, the chord of the wing is constant along the wing’s length. The distance between the leading and trailing edge of the wing, measured parallel to the normal airflow over the wing, is known as the chord. Mean Aerodynamic Chord is the average chord length of a tapered, swept wing.


 0 kommentar(er)
0 kommentar(er)
